Tadeusiewicz sieci neuronowe 2

Przy okazji robienia porządków na dysku, znalazłem drugi artykuł Ryszarda Tadeusiewicza z Entera rocznik 1995 😉 ktoś to jesze pamięta ? Poniżej przedruk.

Jak to jest zbudowane ?

ENTER 2, Styczeń 1995

Ryszard Tadeusiewicz

W poprzednim odcinku opisałem główne elementy zjawiska, jakim jest żywiołowy rozwój mody na sieci neuronowe. Dzisiaj proponuję dokładniejsze poznanie budowy i właściwości tych interesujących systemów.

Sieć neuronowa jest systemem dokonującym określonych obliczeń na zasadzie równoczesnej pracy wielu połączonych ze sobą elementów zwanych neuronami. Neurony traktować można jako elementarne procesory o następujących właściwościach:

1. każdy neuron otrzymuje wiele sygnałów wejściowych i wyznacza na ich podstawie swoją “odpowiedź”, tzn. jeden sygnał wyjściowy,
2. z każdym oddzielnym wejściem neuronu związany jest parametr nazywany wagą (ang. weight); wyraża on stopień ważności informacji docierających tym właśnie wejściem,
3. sygnał wchodzący określonym wejściem jest najpierw przemnażany przez wagę danego wejścia, w związku z czym w dalszych obliczeniach uczestniczy już w formie zmodyfikowanej: wzmocnionej (gdy waga jest większa od 1) lub stłumionej (gdy waga ma wartość mniejszą od 1) względnie nawet przeciwstawnej w stosunku do sygnałów z innych wejść, gdy waga ma wartość ujemną (tzw. wejścia hamujące),
4. po przemnożeniu sygnały wejściowe są w neuronie sumowane, dając pewien pomocniczy sygnał wewnętrzny, nazywany czasem łącznym pobudzeniem neuronu (net va|ye),
5. do tak utworzonej sumy sygnałów? cfedaje niekiedy (nie we wszystkich typach sieci) pewien dodatkowy składnik niezależny od sygnałów; wejściowych, nazywany progiem (bias),
6. suma tak przetworzonych sygnałów może być bezpośrednio traktowana jako sygnał wyjściowy neuronu; w wielu typach sieci – na przykład ADALINE (ADaptive LINEar) to wystarcza. Natomiast w sieciach o bogatszych możliwościach, na przykład MLP (MultiLayer Percep-tron), sygnał wyjściowy neuronu obliczany jest za pomocą pewnej nieliniowej zależności między łącznym pobudzeniem a sygnałem wyjściowym,
7. zależność sygnału wyjściowego od łącznego pobudzenia, zwana charakterystyką neuronu (transfer function) pozwala w każdej chwili jednoznacznie określić sygnał wyjściowy neuronu, jeśli znane są jego sygnały wejściowe. W odróżnieniu od tego, co dzieje się w rzeczywistych neuronach, zwykle zakłada się, że proces ten zachodzi bezzwłocznie, tzn. zmiany sygnałów wejściowych praktycznie natychmiast uwidaczniane są na wyjściu.

Z przytoczonego opisu wynika, że każdy neuron dysponuje pewną wewnętrzną pamięcią (reprezentowaną przez aktualne wartości wag i progu) oraz pewnymi możliwościami przetwarzania sygnałów wejściowych w sygnał wyjściowy. Neuron jest więc stosunkowo prostym, a więc mało kosztownym procesorem i można zbudować system zawierający setki czy tysiące takich elementów.

Mimo że jego możliwości są dość ograniczone, to jednak okazują się one wystarczające do zbudowania systemów realizujących bardzo złożone zadania przetwarzania danych. Ponieważ zasób informacji gromadzonych przez pojedynczy neuron jest ograniczony, zaś jego możliwości obliczeniowe ubogie, sieć neuronowa może działać wyłącznie jako całość. Jak z tego wynika, wszystkie omówione w poprzednim odcinku możliwości i właściwości sieci neuronowych są wynikiem kolektywnego działania bardzo wielu połączonych ze sobą elementów: całej sieci, a nie pojedynczych neuronów. Tak więc spotykana niekiedy nazwa MPP (Massive Parallel Processing) , z jaką wiąże się cała ta dziedzina informatyki, jest najzupełniej uzasadniona.

Zainteresujmy się teraz funkcjonowaniem całej sieci neuronowej. Jak wynika z przytoczonych wyżej uwag, program działania, informacje stanowiące bazę wiedzy, dane, na których wykonuje się obliczenia oraz sam proces obliczania – są w sieci całkowicie rozproszone. Nie da się wskazać miejsca, w którym zgromadzona jest w niej taka lub inna konkretna informacja (chociaż sieci bywają wykorzystywane jako pamięci, zwłaszcza tzw. pamięci skojarzeniowe i bardzo dobrze spełniają swoje zadania).

Podobnie niemożliwe jest zlokalizowanie w określonym miejscu sieci jakiegoś wydzielonego fragmentu wykonywanego algorytmu, np. wskazanie, które elementy sieci odpowiedzialne są za wstępne przetwarzanie i analizę wprowadzanych danych, a które dostarczają końcowego rozwiązania. Sieć działa zawsze jako całość i wszystkie jej elementy mają swój wkład w realizację wszystkich czynności, które sieć realizuje.

Podobnie się dzieje np. przy odtwarzaniu hologramu, gdzie z każdego kawałka rozbitej płyty fotograficznej można odtworzyć cały obraz sfotografowanego (sholografowanego?) przedmiotu. Jedną z konsekwencji tej właściwości sieci jest jej niewiarygodna zdolność do poprawnego działania nawet po uszkodzeniu znacznej części wchodzących w jej skład elementów.

Struktura sieci powstaje w ten sposób, że wyjścia jednych neuronów łączy się (według wybranego schematu) z wejściami innych, tworząc łącznie system zdolny do równoległego, w pełni współbieżnego przetwarzania różnych informacji. Oczywiście konkretna topologia sieci, to znaczy liczba procesorów i sposób ich połączenia, powinny wynikać z rodzaju zadania, jakie zamierzamy sieci postawić.

Związek między rodzajem zadania a topolgią sieci nie jest tak jednoznaczny, jak by się mogło wydawać. W bogatej literaturze dotyczącej sieci znaleźć bowiem można prace, w których wykazano, że w istocie decyzje dotyczące struktury sieci wpływają na jej zachowanie znacznie słabiej niż by można było oczekiwać. To paradoksalne stwierdzenie wynika z faktu, że zachowanie sieci w zasadniczy sposób determinowane jest przez proces jej uczenia, a nie przez strukturę czy liczbę użytych do jej budowy elementów. Oznacza to, że sieć mająca zdecydowanie gorszą strukturę, lecz dobrze nauczona może znacznie skuteczniej rozwiązywać postawione zadania niż źle trenowana sieć o optymalnie dobranej strukturze. Znane są doświadczenia, w których strukturę sieci wybierano całkowicie przypadkowo (ustala-

Każdy neuron dysponuje pewną wewnętrzną pamięcią oraz pewnymi możliwościami przetwarzania sygnałów wejściowych w sygnal wyjściowy. Neuron jest stosunkowo prostym i tanim procesorem. Można zbudować system zawierający setki czy tysiące takich elementów.

jąc na drodze losowania, które elementy należy ze sobą połączyć i w jaki sposób), a sieć mimo to zdolna była do rozwiązywania stawianych jej trudnych zadań! Oznacza to, że proces uczenia mógł tak dostosować jej parametry do realizacji zadanego algorytmu, że proces rozwiązywania zadania przebiegał poprawnie mimo całkowicie losowej struktury sieci. Te doświadczenia, wykonane po raz pierwszy przez Franka Rosenblatta na początku lat 70. i potem wielokrotnie powtarzane, dowiodły, że pochodząca jeszcze od Arystotelesa i rozwinięta potem przez Locke’a koncepcja tabula rasa – umysłu rodzącego się jako pusta, nie zapisana karta, zapełniana dopiero w trakcie nauki i gromadzenia doświadczeń – jest technicznie możliwa do realizacji w formie sieci neuronowej.

Odrębnym zagadnieniem jest próba odpowiedzi na pytanie, czy tak właśnie jest z realnym umysłem konkretnego człowieka? Czy istotnie, jak utrzymywał Locke, wrodzone uzdolnienia są niczym, a zdobyta w procesie nauki wiedza – wszystkim?

Nie wiemy tego na pewno, ale chyba tak nie jest. Natomiast wiemy z całą pewnością, że sieci neuronowe mogą całą swoją wiedzę zyskiwać wyłącznie w trakcie nauki i nie muszą mieć z góry zadanej, precyzyjnie określonej struktury dopasowanej do stawianych im zadań. Oczywiście sieć musi mieć wystarczający stopień złożoności, żeby w jej strukturze można było w toku uczenia wykrystalizować potrzebne połączenia i struktury.

Zbyt mała sieć nie jest w stanie nauczyć się niczego, gdyż jej “potencjał intelektualny” na to nie pozwala – rzecz jednak nie w strukturze, a w liczbie elementów. Szczura nikt nie uczy teorii względności, chociaż można go wytresować w rozpoznawaniu drogi wewnątrz skomplikowanego labiryntu. Podobnie nikt się nie rodzi “zaprogramowany” do tego, by być wyłącznie genialnym chirurgiem lub koniecznie tylko budowniczym mostów – o tym decydują specjalistyczne studia – chociaż niektórym ludziom wystarcza intelektu zaledwie do tego, by ładować piasek na ciężarówkę, a i to pod nadzorem. Tak już jest i żadne frazesy na temat równości nie są w stanie tego zmienić. Jedni mają wystarczające zasoby intelektualne, inni nie – podobnie jak jedni mają okazałą muskulaturę, a inni wyglądają jakby… zbyt długo przesiadywali przed monitorem komputera.

W przypadku sieci sytuacja jest podobna – nie można spowodować, by sieć z góry miała jakieś szczególne uzdolnienia, można jednak łatwo wyprodukować cybernetycznego kretyna, który nigdy się niczego nie nauczy, bo ma za małe możliwości. Struktura sieci może więc być dowolna, byle była dostatecznie duża. Wkrótce dowiemy się także, że nie powinna być zbyt duża, bo to także szkodzi – ale o tym za chwilę.

Niezależnie od przytoczonych uwag jakąś strukturę trzeba sieci nadać, zwłaszcza że wybór rozsądnej struktury, dobrze dopasowanej do specyfiki zadania, może w istotny sposób skracać czas uczenia i polepszać końcowe wyniki – dlatego pewne uwagi na ten temat muszę tu przedstawić. Zresztą wszyscy wiemy, jak trudne rozterki wiążą się czasem z wyborem dowolnego, nie narzuconego z góry rozwiązania. Postawienie konstruktora sieci w sytuacji, kiedy może przyjąć dowolną jej organizację, jest podobne do dylematów początkujących informatyków, z zakłopotaniem wpatrujących się w komunikat “Press any key…”. Który to jest ten dowolny klawisz?!

Można się z tego śmiać, ale dla mnie podobnie brzmi często zadawane przez moich studentów i doktorantów, pełne rozpaczy pytanie: no dobrze, ale jaka to jest ta “dowolna struktura sieci”?

Powiem teraz kilka słów o możliwych i często spotykanych strukturach sieci, wyraźnie akcentując, że podane niżej informacje i propozycje nie wyczerpują wszystkich możliwości. Przeciwnie, każdy badacz może i powinien być tu swoistym Demiurgiem, twórcą i kreatorem nowych bytów, gdyż właściwości sieci o różnych strukturach nie są jeszcze dostatecznie poznane. Jest to praca, przy której przyda się każda para półkul mózgowych.

Najpierw dokonam pewnego podziału struktur często stosowanych sieci neuronowych na dwie ważne klasy. Z jednej strony będziemy rozważać struktury nie zawierające sprzężeń zwrotnych, a z drugiej – struktury, które takie sprzężenia zawierają. Pierwsze z wymienionych sieci określane są często terminem feedforward, drugie natomiast bywają wiązane z nazwiskiem Hopfielda.

Nie da się wskazać w sieci miejsca, w którym zgromadzona jest taka lub inna informacja. Podobnie niemożliwe jest zlokalizowanie w określonym miejscu sieci wydzielonego fragmentu wykonywanego algorytmu.

Sieci feedforward to struktury, w których istnieje ściśle określony kierunek przepływu sygnałów – od pewnego ustalonego wejścia (na którym podaje się sieci sygnały będące danymi wejściowymi, precyzującymi zadania, które mają być rozwiązywane), do wyjścia, na którym sieć podaje ustalone rozwiązanie. Takie sieci są najczęściej stosowane i najbardziej użyteczne. Ich obszerniejsze omówienie stanowić będzie treść dalszej części tego artykułu i kilku następnych.

Sieci Hopfielda cechują się natomiast tym, że neurony tworzą sprzężenia zwrotne, liczne i skomplikowane zamknięte pętle, w których impulsy mogą długo krążyć i zmieniać się, zanim sieć osiągnie pewien stan ustalony – o ile go w ogóle osiągnie. Analiza właściwości i możliwości sieci Hopfielda jest znacznie bardziej złożona niż w przypadku sieci feedforward, ale też możliwości obliczeniowe tych sieci są fascynująco odmienne od możliwości innych typów sieci. Na przykład, są one zdolne do znajdowania rozwiązań problemów optymalizacyjnych, czyli szukania najlepszych rozwiązań pewnych klas zadań, czego sieci feedforward z reguły robić nie potrafią. Swojego czasu prawdziwą sensacją było uzyskanie za pomocą sieci Hopfielda rozwiązania słynnego problemu komiwojażera, co otworzyło dla tych sieci obszerną i ważną klasę problemów obliczeniowych NP-zupełnych. Jednak budowa sieci ze sprzężeniami zwrotnymi jest bez wątpienia zadaniem trudniejszym i bardziej skomplikowanym niż korzystanie z sieci feedforward. Ponadto, trudniej zapanować nad siecią, w której kłębi się parę tysięcy równoległych, dynamicznych procesów niż nad siecią, w której sygnały grzecznie i spokojnie przepływają od wejścia do wyjścia. Dlatego warto zaczynać znajomość z sieciami neuronowymi właśnie od sieci z jednokierunkowym przepływem sygnałów, stopniowo i powoli przechodząc do sieci Hopfielda.

Skupiając uwagę na sieciach feedforward możemy stwierdzić, że do opisania ich struktury stosunkowo wygodny jest model warstwowy. W modelu tym zakłada się, że neurony zgrupowane są w pewne zespoły (warstwy), tak zorganizowane, że główne połączenia i związane z nimi przepływy sygnałów odbywają się pomiędzy elementami sąsiednich warstw. Jak już wspominałem, połączenia między neuronami sąsiednich warstw mogą być kształtowane na wiele sposobów, wedle uznania twórcy sieci, jednak najczęściej korzysta się ze schematu połączeń typu “każdy z każdym”, licząc na to, że proces uczenia doprowadzi do samorzutnego “wykrystalizowania się” potrzebnego zbioru połączeń – po prostu na wejściach, które okażą się zbyteczne z punktu widzenia rozwiązywanego zadania, proces uczenia ustawi współczynniki (wagi) równe zeru, co w praktyce przerwie niepotrzebne połączenia.

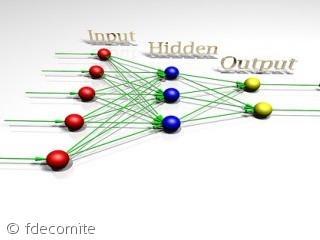
Wśród warstw neuronów budujących sieć neuronową może być wyróżniona warstwa wejściowa. Warstwa ta otrzymuje dane z zewnątrz sieci – tą drogą wprowadzane są zadania podlegające rozwiązywaniu. Przy projektowaniu tej warstwy twórca sieci ma ułatwioną decyzję, liczba elementów tej warstwy jest bowiem ściśle zdeterminowana przez liczbę danych wejściowych, które trzeba brać pod uwagę przy rozwiązywaniu określonego zadania.

Inna rzecz, że czasem określenie, ile i jakie dane należy wprowadzać do sieci, by poradziła sobie ona ze stawianym zadaniem, nie jest sprawą łatwą, na przykład w zadaniu prognozowania kursów akcji na giełdzie. Wiadomo, że niektórzy badacze osiągają tu zachęcające wyniki przynoszące bardzo duże korzyści inwestorom, którzy w oparciu o produkowane przez sieć prognozy podejmują decyzje o zakupie lub sprzedaży określonych walorów. Jednak publikacje na ten temat są bardzo powściągliwe w ujawnianiu, jakie dane stanowiły punkt wyjścia prowadzonych obliczeń. Owszem, mówi się o tym, że stosowano sieć, że ją uczono (podaje się nawet algorytm uczenia), podaje się wyniki: jak wiele zyskano dzięki trafnym inwestycjom, jak dokładnie sieć prognozowała zmiany kursów akcji – tu możliwe są bardzo ładne wykresy linii rzeczywistych zmian i linii prognoz. Natomiast w odniesieniu do danych wejściowych mówi się tylko, że podawano informacje dotyczące wcześniejszych zmian notowań akcji oraz wyniki analiz finansowych notowanych na giełdzie spółek. Jak te dane preparowano i w jakim stopniu wykorzystano – autorzy jakoś zapominają napisać. Takie roztrzepane gapy!

Inna wyróżniona warstwa produkuje sygnały wyjściowe z całej sieci, stanowiące rozwiązania stawianych sieci zadań. Tu sytuacja jest prostsza, gdyż na ogół wiemy, ilu i jakich rozwiązań potrzebujemy. Jest jednak pewna subtelność, na którą warto zwrócić uwagę. Otóż neurony dysponują wprawdzie możliwością dostarczania rozwiązania w postaci pewnej wartości liczbowej, jednak wartość ta podlega pewnym dość istotnym ograniczeniom. Na przykład w większości implementacji sieci sygnały wyjściowe wszystkich neuronów mogą przyjmować wartości z przedziału od O do l, zatem jeśli potrzebne nam wyniki mają mieć wartości z innego (zwykle szerszego) przedziału, konieczne jest pewne skalowanie. Jakby tego było mało, pojawia się inne ograniczenie: wyniki dostarczane przez sieć mają zawsze charakter przybliżony. Jakość tego przybliżenia może być różna, jednak o dokładności wielu cyfr znaczących nie może tu być mowy – dobrze, jeśli wynik dostarczany przez neuron ma dokładność lepszą niż dwie cyfry, czyli błąd może sięgać kilku procent. Taka jest już po prostu natura tego narzędzia.

Świadomość występowania podanych ograniczeń zmusza do odpowiedniej interpretacji sygnałów wyjściowych, by można było z nich sensownie korzystać. Najwygodniej jest tak interpretować stawiane neurokomputerowi zadania, by odpowiedź mogła mieć charakter zaklasyfikowania do określonej kategorii. Na przykład, można domagać się, by sieć określiła, czy zyskowność inwestycji jest “mała” “średnia” lub “duża”, względnie czy kredytobiorca jest “pewny”, “ryzykowny” czy

Sieć mająca zdecydowanie gorszą strukturę, lecz dobrze nauczona, znacznie skuteczniej rozwiązuje postawione zadania niż źle trenowana sieć o optymalnie dobranej strukturze.

“zupełnie niewiarygodny”. Natomiast wymaganie dokładnego określenia stopnia ryzyka lub wysokości kwoty, jaką można komuś pożyczyć, prowadzić będzie niezawodnie do frustracji. Dlatego liczba wyjść z budowanej sieci bywa często większa niż liczba pytań, na które poszukujemy odpowiedzi, ponieważ dla wielu sygnałów wyjściowych trzeba sztucznie wprowadzić kilka neuronów obsługujących dane wyjście. Na przykład przewidywany przedział wartości sygnału wyjściowego zostaje podzielony na pewne podzakresy i poszczególne neurony wyjściowe odpowiedzialne są za sygnalizowanie przynależności aktualnego rozwiązania do określonego przedziału. Tworzenie sieci, z której “wyciska się” dokładne rozwiązania problemów matematycznych, jest typową “sztuką dla sztuki” -czasochłonną zabawą o minimalnej przydatności praktycznej. Trzeba by stosować symulatory sieci dysponujące bardzo dobrą dokładnością numeryczną, lecz zalety sieci neuronowych stają się wówczas co najmniej problematyczne.

Każda sieć feedforward musi mieć przynajmniej dwie wymienione wyżej warstwy: wejściową i wyjściową. Jednak wiele sieci, (zwłaszcza tych rozwiązujących bardziej złożone zadania musi dysponować dodatkowymi warstwami elementów, pośredniczących pomiędzy wejściem i wyjściem. Warstwy te nazywane są zwykle (ze względów, o których będzie mowa) warstwami ukrytymi. Tworzą one dodatkową strukturę przetwarzającą informację w sieciach neuronowych, a ich rolę najłatwiej jest przedyskutować na przykładzie sieci realizujących często pojawiające się zadanie rozpoznawania obrazów.

W sieciach takich na wejście (do pierwszej warstwy) podaje się obraz w postaci zbioru pikseli odczytanych przez skaner lub Frame Grabber. W takim przypadku wejściowa warstwa neuronów odpowiada swymi rozmiarami i organizacją (zgrupowaniem neuronów w odpowiednie wiersze i kolumny) organizacji samego obrazu: do każdego punktu obrazu przypisany jest neuron, który analizuje i sygnalizuje jego stan. Na wyjściu oczekuje się decyzji informujących o tym, co rozpoznano. Na przykład może być ona tak zorganizowana, że do poszczególnych neuronów wyjściowych przypiszemy umownie pewne decyzje – na przykład “rozpoznano literę A”, “rozpoznano literę B” itp., a wielkości sygnałów na tych wyjściach interpretować się będzie w kategoriach stopnia pewności odpowiedniej decyzji. Łatwo zauważyć, że możliwe jest w związku z tym podawanie przez sieć odpowiedzi wieloznacznych (“to coś jest podobne w stopniu 0,7 do litery A, ale w stopniu 0,4 przypomina także literę B”). Jest to jedna z ciekawych i użytecznych cech sieci neuronowych, które można w związku z tym kojarzyć z systemami o rozmytej (fuzzy) logice działania – obszerniejsze omówienie tego aspektu znajdzie miejsce w jednym z późniejszych artykułów cyklu.

Neurony warstwy ukrytej pełnią w omawianej tu sieci rolę pośredników – mają one bezpośredni dostęp do danych wejściowych, czyli oglądają pokazany sieci obraz, a na podstawie ich wyjść dalsze warstwy podejmują określone decyzje o rozpoznaniu takiego lub innego obrazu. Dlatego uważa się, że rola neuronów warstwy ukrytej polega na tym, by pośredniczyły między wejściem i wyjściem oraz wypracowywały zestawy wstępnie przetworzonych danych wejściowych, z których korzystać będą neurony dalszych warstw przy określaniu końcowego wyniku. Przydatność warstw pośrednich wynika z faktu, że na ogół dokonanie pewnych przekształceń danych wejściowych sprawia, że rozwiązanie stawianego przed siecią zadania staje się istotnie łatwiejsze niż w przypadku próby rozwiązywania zadania w sposób bezpośredni. Na przykład w zadaniach rozpoznawania obrazów trudno jest czasem znaleźć regułę pozwalającą ustalić, jaki obiekt pokazano, analizując bezpośrednio same jasne i ciemne pi-ksele obrazu. Ten sam obiekt może bowiem mieć zupełnie inne wartości pikseli w pewnych wybranych punktach (jeśli jest na przykład przesunięty), zaś zupełnie różne obiekty mogą mieć na cyfrowych obrazach bardzo duże zbiory identycznych pikseli. Oczekiwanie, że sieć neuronowa “jednym skokiem” pokona wszystkie te trudności jest więc mało realistyczne. Na ogół żaden proces uczenia nie zdoła zmusić prostej dwuwarstwowej sieci do tego, by raz rozumiała te same zestawy pikseli jako należące do różnych obiektów, a innym razem kojarzyła różne zestawy pikseli z tym samym obiektem. Tego po prostu nie da się zrobić.

To, czego nie może zrobić sieć o mniejszej liczbie warstw, na ogół potrafi wykonać sieć zawierająca odpowiednie warstwy ukryte. W takich zadaniach neurony tych warstw będą znajdowały pewne wartości pomocnicze, na przykład ogólne cechy opisujące strukturę obrazu i widocznych na nim obiektów. Cechy te powinny lepiej odpowiadać wymaganiom związanym z ostatecznym rozpoznaniem obrazu niż sam oryginalny obraz – na przykład mogą być w pewnym stopniu niezależne od położenia czy skali rozpoznawanych obiektów.

Należy podkreślić, że twórca sieci nie musi sam jawnie określać, jakie to cechy obrazu mają być znajdowane, gdyż sieć może sama nabywać stosownych umiejętności w trakcie procesu uczenia. Trzeba jej jednak dać szansę poprzez uwzględnienie w strukturze elementów, które mogą właśnie takie “opisowe cechy obrazu” wydobywać. Sam charakter wydobywanych cech nie jest zdeterminowany przez strukturę sieci, tylko przez proces uczenia. Jeśli wyobrazimy sobie sieć, która ma rozpoznawać obrazy, to cechy, które będą wydobywały neurony warstwy ukrytej dostosują się automatycznie do rodzaju rozwiązywanego zadania. Jeśli nakażemy sieci wykrywanie na zdjęciach lotniczych obrazów zamaskowanych wyrzutni rakietowych, to staje się oczywiste, że głównym zadaniem warstwy ukrytej będzie uniezależnienie się od położenia obiektu, gdyż podejrzany kształt może się pojawić w dowolnym rejonie obrazu i zawsze powinien być tak samo rozpoznany. Jeśli natomiast sieć ma rozpoznawać litery, to nie powinna gubić informacji o ich położeniu – mało przydatna będzie sieć, która poinformuje nas, że gdzieś tam na zeskanowanej stronicy znajduje się litera A – my musimy wiedzieć, gdzie ona jest, a dokładniej – w jakim kontekście występuje. Natomiast celem warstwy ukrytej może być wydobycie cech pozwalających na niezawodne rozpoznanie litery niezależnie od jej rozmiaru i od kroju czcionki (font). Co ciekawe, po odpowiednim treningu oba te zadania może rozwiązywać ta sama sieć, chociaż oczywiście sieć nauczona rozpoznawać czołgi nie potrafi odczytywać pisma, a nauczona identyfikować odciski palców nie poradzi sobie z rozpoznawaniem twarzy.

Jak wynika z przytoczonych uwag, najszersze możliwości zastosowań posiadają sie?ci mające przynajmniej trójwarstwo-wą strukturę, z wyróżnioną warstwą wejściową przyjmującą sygnały, warstwą ukrytą wydobywającą potrzebne cechy wejściowych sygnałów oraz z warstwą wyjściową podejmującą ostateczne decyzje i podającą rozwiązanie. W tej strukturze pewne elementy są zdeterminowane: liczba elementów wejściowych i wyjściowych, a także zasada połączeń (każdy z każdym) pomiędzy kolejnymi warstwami. Są jednak elementy

Nadmierna liczba elementów warstwy ukrytej Ł if prowadzi do efektu “uczenia się na pamięć”. Sieć ucząc się na podstawie przykladów poprawnych rozwiązań nie podejmuje próby uogólniania nabywanych wiadomości, tylko dysponując bardzo pojemną pamięcią usiłuje osiągać sukces na zasadzie dokładnego zapamiętania reguł w rodzaju: “przy takim wejściu takie wyjście”.

zmienne, które trzeba wybrać samemu: liczba warstw ukrytych (jedna czy kilka?) oraz liczba elementów w warstwie (warstwach?) ukrytych. Ponieważ brakuje precyzyjnej teorii sieci neuronowych, elementy te wybiera się zwykle arbitralnie, co jednak nie powinno mieć (w pewnym zakresie) wpływu na sposób działania sieci, gdyż w trakcie procesu uczenia ma ona możliwość korygowania ewentualnych błędów struktury poprzez wybór odpowiednich parametrów połączeń.

Trzeba jednak wyraźnie przestrzec przed dwoma rodzajami błędów, stanowiących pułapki dla wielu (zwłaszcza początkujących) badaczy sieci neuronowych. Pierwszy błąd-polega na zaprojektowaniu sieci o zbyt małej liczbie elementów – jeśli warstwy ukrytej nie ma lub występuje w niej zbyt mało neuronów, proces uczenia może się definitywnie nie udać, gdyż w zbyt ubogiej strukturze sieć nie ma szans odwzorować wszystkich niuansów rozwiązywanego zadania.
Niestety, nie można także “przedobrzyć”. Zastosowanie zbyt wielu warstw ukrytych prowadzi do znacznego pogorszenia sprawności procesu uczenia. Często lepsze wyniki daje sieć o mniejszej liczbie warstw ukrytych (bo można ją porządnie nauczyć) niż teoretycznie lepsza sieć z większą liczbą warstw ukrytych, w której jednak proces uczenia “grzęźnie” w nadmiarze szczegółów. Dlatego należy stosować sieci o jednej lub dwóch warstwach ukrytych, natomiast pokusę stosowania większej liczby warstw ukrytych najlepiej przezwyciężać stosując post i zimne kąpiele.

Jeszcze gorsza sytuacja pojawia się przy szacowaniu liczby neuronów wymaganych do prawidłowego działania warstwy ukrytej. Wiemy już, jakie są zadania tych elementów – mają one wypracować pewne pomocnicze dane pośrednie, dzięki którym znalezienie rozwiązań stanie się łatwiejsze niż w oparciu o same dane wejściowe. Jednak ta wiadomość wcale nie pomaga w określeniu, ile ma być tych elementów. Na pewno nie może ich być zbyt mało, ale co się stanie, jeśli będzie ich za dużo?

Okazuje się, że nadmierna liczba elementów warstwy ukrytej prowadzi do niekorzystnego efektu nazywanego “uczeniem się na pamięć”. Polega on na tym, że sieć ucząc się na podstawie przedstawianych jej przykładów poprawnych rozwiązań stawianych jej zadań nie podejmuje próby uogólniania nabywanych wiadomości, tylko dysponując bardzo pojemną pamięcią (dzięki posiadaniu rozległej warstwy ukrytej) usiłuje osiągać sukces na zasadzie dokładnego zapamiętania reguł w rodzaju “przy takim wejściu takie wyjście”. Objawem takiego nieprawidłowego działania sieci jest fakt, że uczy się ona dokładnie i szybko całego tzw. ciągu uczącego (czyli zbioru przykładów użytych do pokazania sieci, jak należy rozwiązywać stawiane zadania), natomiast fatalnie kompromituje się przy pierwszej próbie egzaminu, czyli rozwiązania zadania z podobnej klasy, nieco jednak odmiennego od zadań jawnie pokazywanych w trakcie uczenia. Przykładowo, ucząc sieć rozpoznawania liter bardzo szybko uzyskujemy sukces (sieć bezbłędnie rozpoznaje wszystkie pokazywane jej litery), ale próba pokazania jej litery napisanej odmiennym charakterem pisma lub wydrukowanej innym fontem prowadzi bądź do zupełnego braku rozpoznania (zera na wszystkich wyjściach) bądź do rozpoznań ewidentnie błędnych. Bliższa analiza wiedzy zgromadzonej przez sieć ujawnia w takich przypadkach, że zapamiętała ona wiele prostych reguł w rodzaju “jak tutaj są dwa piksele zapalone, a tam jest pięć zer – to należy rozpoznać literę A”. Te prymitywne reguły nie wytrzymują oczywiście konfrontacji z nowym zadaniem i sieć zawodzi nasze oczekiwania.

Opisany objaw “uczenia się na pamięć” nie występuje w sieciach mających mniejszą warstwę ukrytą, gdyż dysponując ograniczoną pamięcią sieć taka musi lepiej się starać i wypracować na niewielu dostępnych jej elementach warstwy ukrytej takie reguły przekształcania wejściowego sygnału, by umożliwić jego trafne wykorzystanie w więcej niż jednym przypadku wymaganej odpowiedzi systemu. Z reguły prowadzi to do znacznie wolniejszego i bardziej uciążliwego procesu uczenia (przykłady, na podstawie których sieć ma się uczyć, muszą być pokazane więcej razy – często kilkaset lub kilka tysięcy razy), jednak efekt końcowy jest zwykle znacznie lepszy – z chwilą stwierdzenia dobrego działania sieci dla przykładów stanowiących podstawę uczenia mamy prawo przypuszczać, że poradzi sobie ona także z podobnymi, chociaż nie identycznymi, zadaniami, pokazanymi jej w trakcie egzaminu. Nie zawsze tak jest, ale zwykle tak bywa i na tym musimy opierać swoje oczekiwania dotyczące użycia sieci.

Kilka następnych artykułów poświęcę studiowaniu mechanizmów uczenia i działania sieci neuronowych, oczywiście na takim poziomie i w takim zakresie, w jakim będzie to możliwe bez odwoływania się do matematyki. Czytelników zainteresowanych bliższymi szczegółami odsyłam do mojej książki pt. “Sieci neuronowe” dostępnej obecnie w prawie każdej księgarni.